Entertainment
January 26, 2024
Ed McMahon Publishers Clearing House Connection Sparks ‘Mandela Effect’ Blame
Ed McMahon Publishers Clearing House Longtime television partner Johnny Carson According to some TV fans, Ed McMahon once served as…
Entertainment
December 20, 2023
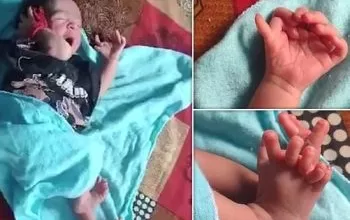
Baby born with 26 fingers and toes in India is dubbed reincarnation of Hindu goddess
The reincarnation of a Hindu goddess has been suggested for a newborn baby born in India with 26 fingers and…
Lifestyle
December 19, 2023
Amuru Abam
Amuru Abam is a small but mighty community in Abam, in Arochukwu LGA of Abia State, Nigeria. It is in…
Entertainment
December 19, 2023
Gary Plauché, The Louisiana Dad Who Took Deadly Revenge On His Son’s Rapist On Live Television
A parent’s biggest nightmare is probably having their child kidnapped or sexually assaulted. After enduring both, Baton Rouge, Louisiana-based American…
Entertainment
December 19, 2023
Chinese livestreamer Brother Three Thousand who gained fame for his drinking challenges is found dead
Chinese livestreamer Brother Three Thousand who gained fame for his drinking challenges is found dead after downing seven bottles of…
Entertainment
December 19, 2023
Gloria Satterfield Autopsy Results Revealed Online
Since Gloria Satterfield’s unfortunate passing in 2020, her death has generated a great deal of debate. At the home of…
Entertainment
December 19, 2023
Daniel Tibia Death – The Story of Gabriel Kuhn and Daniel Petry
Both 12-year-olds Gabriel Kuhn and Daniel Petry had a passion for the video game Tibia. The lives of the two…
Health & Wellness
December 19, 2023
Why does Farting feel good? Here are 6 reasons
Farting, also known as passing gas or flatulence, is a natural bodily function that can evoke various reactions from embarrassment…
How To
December 19, 2023
10 Ways to Prevent Flooding In Your Community
Flooding is a natural disaster that can have devastating consequences on communities, infrastructure, and the environment. As climate change intensifies,…
Celebrities
December 19, 2023
What happened to Solidstar? Solidstar Health update
Nigerian singer Joshua Iniyezo, popularly known by his stage name Solidstar, is battling mental health issues, his younger brother Joseph…