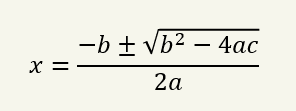
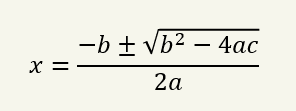
Quadratic Expressions and Equations are common in general mathematics. The use of the formula approach is one method for tackling such situations. Because this method can solve any basic quadratic equation, it was dubbed the “almighty formula.” I had heard of the almighty formula long before I began learning or even hearing about quadratic equations.
I assumed that the formula would be capable of solving all mathematical difficulties. Some children continue to struggle with quadratic equations. Discover how it was created and how to apply it to solve problems.
General quadratic equation
The general expression for a quadratic expression is given as:
aX² + bX + c = 0
It is from this expression that the almighty formula was derived. To get it, we will use the method known as completing the square. Below is the step-by-step guide:
Step 1:
Move the constant to the right-hand side
aX² + bX = –c
Step 2
Divide by the coefficient of X²
Step 3
Divide the coefficient of X by 2 and square it (the coefficient of X is b/a). This makes the left-hand side a perfect square.
b/a divide by 2 is b/2a and squaring it is (b/2a)². Add this to both sides of the equation.
Step 4
Add (b/2a)² to both side of the equation
Step 5
Expand the bracket on the right-hand side, this gives b²/4a².
Step 6
Since the left-hand side is a perfect square, the left-hand side will then look like this
Step 7
On the right-hand side, find the LCM of both fractions
The result is
Step 8
According to the laws of indices, square both sides. The result is given below
Step 9
Also from the law of indices, the 4a² will become 4a because the root will cancel out the square. The result is
Step 10
Take b/2a to the right-hand side and find the LCM.
The result is what we call the almighty formula but it is actually called the quadratic formula.
Methods used to solve a quadratic equation
There are four different methods that can be used to solve a quadratic equation. Which are:
1. Factorization;
2. Completing the square;
3. The general quadratic formula;
4. Graphical solution.
Each of the four methods above can be used to solve specific types of quadratic equations, however, our main focus shall be to apply the general quadratic formula, also known as the “Almighty Formula.”.
As the alias implies, it can be used to solve any standard quadratic equation. This formula works where all else has failed.
For a standard quadratic equation of the form: ax2 + bx + c = 0;
EXAMPLE: Solve 4x2-11x – 21 = 0
See more examples here:
